Wat zijn kwadratische functies en hoe los je ze op?
Kwadraten komen niet alleen bij wiskunde voor, zoals bij de stelling van Pythagoras, maar ook bij alle andere exacte wetenschappen. Maar wat is een kwadraat precies? en hoe los je een kwadratische vergelijking op? Dat lees je in deze blog.
Kwadratische functies komen voor in verschillende vakgebieden zoals bij het berekenen van oppervlaktes in de wiskunde en bij de kwadratenwet in de natuurkunde. In deze blog leer je hoe je een kwadratische functie oplost. Benieuwd naar andere functies? Lees dan deze blog.
Wat is een kwadraat?
Een kwadraat is de tweede macht en betekent dat de waarde met zichzelf wordt vermenigvuldigd.
Voorbeeld: en spreken we uit als ‘vier kwadraat’.
Een functie is kwadratisch wanneer de onbekende letter in het kwadraat staat én wanneer er geen andere in de functie is met een hogere macht dan twee.
De standaardfunctie is .
Hierin zijn en getallen en is de onbekende. Als je van zo’n kwadratische functie een grafiek maakt is dat altijd een parabool. Er zijn twee typen parabolen, een dal- en bergparabool.
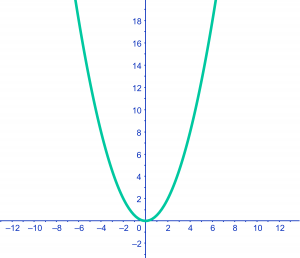
Dalparabool ()
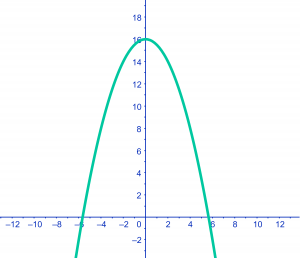
Bergparabool ()
Hoe los je een kwadratische vergelijking op?
Voor het oplossen van een kwadratische vergelijking zijn er drie mogelijkheden. Daarvoor is het belangrijk dat je goed kijkt uit welke variabelen de kwadratische vergelijking bestaat. Hier volgen de mogelijkheden.
Optie 1:
Wanneer de vergelijking alleen uit de variabelen en uit de standaardfunctie bestaat, los je de vergelijking als volgt op.
Voorbeeld: 2
Stap 1: haal naar de rechter kant van het =-teken.
Stap 2: Deel links en rechts van het =-teken door .
Stap 2: Neem links en rechts de wortel. Let op: het kwadraat van -2 is ook 4!
Optie 2:
Wanneer de kwadratische vergelijking een waarde van heeft, los je de vergelijking als volgt op:
Voorbeeld:
Stap 1: haal buiten haakjes.
Stap 2: stel dat één van beide termen 0 is.
Stap 3: Los op.
Optie 3:
Er zijn twee methoden voor het oplossen van kwadratische vergelijkingen die uit drie termen bestaan:
- De product-som-methode
- De abc-formule.
Eerst probeer je of de product-som-methode een optie is. Hiervoor ga je de functie omschrijven naar . Om en te bepalen ga je opzoek naar twee getallen waarbij en .
Voorbeeld 1:
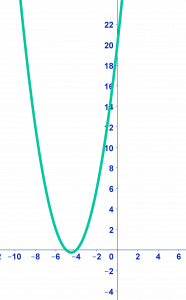
Stap 1. Ga opzoek naar twee getallen die samen op uitkomen en met elkaar vermenigvuldigd op .
en
dus en
Stap 2. Vul de gevonden en in.
Stap 3. Los de vergelijking op. Voor elke oplossing wil je dat een stukje tussen haakjes uitkomt op 0.
Bij sommige vergelijkingen kan het natuurlijk gebeuren dat je een vergelijking krijgt waarbij je geen en kan vinden. In die gevallen gebruik je de welbekende abc-formule. Hiervoor bereken je eerst de discriminant:
Voor de discriminant geldt:
- Als , dan zijn er twee snijpunten met de -as.
- Als , dan raakt de functie de -as en is er dus één snijpunt.
- Als , dan zijn er geen snijpunten met de -as.
Als je de discriminant hebt uitgerekend kun je deze invullen in de abc-formule om de oplossingen voor te berekenen:
Voorbeeld 2:
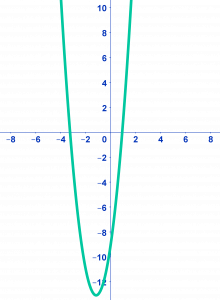
Stap 1: Bereken de discriminant.
dus de vergelijking heeft twee oplossingen.
Stap 2: Vul de abc-formule in.
Stap 3: Los op.
Tip
Je kunt een opgave over kwadratische vergelijkingen herkennen aan een kwadraat in de vergelijking of een parabool als grafiek.
Let op: het kwadraat van een negatief getal geeft een positieve uitkomst!
Voorbeeldopgaven

Basis
Los de vergelijking algebraïsch op.
Uitwerking
Eerst ga je proberen of de product-som-methode een optie is.
en dus en
De oplossingen zijn en
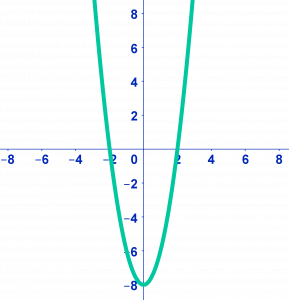
Je kunt je antwoord altijd nagaan door de grafiek te tekenen in je GR:
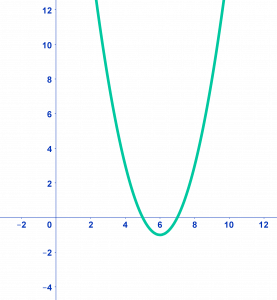
Je kunt dan zien dat de oplossingen en kloppen.

Gevorderd
Los de vergelijking op en geef aan of het een dal- of bergparabool is. Rond je antwoord af op twee decimalen.
Uitwerking
De grafiek is en dalparabool want en
Er zullen dus twee oplossingen zijn.
De oplossingen zijn en
Dit vind je ook interessant
Mis jij nog een bètavak?
Heb jij een bètavak nodig om toegelaten te worden tot een hbo-opleiding of de universiteit? Onze cursussen wiskunde a, wiskunde b, natuurkunde, scheikunde of biologie behandelen de gehele bovenbouwstof. We bereiden je optimaal voor het halen van een deelcertificaat of het CCVX voortentamen. Zo kun je alsnog worden toegelaten tot jouw studie naar keuze!
Vraag een informatiepakket aan
Wil je meer weten over ons cursusaanbod? Vraag dan een gratis informatiepakket aan en lees alles rustig door!